暇なときに頭の体操になるクイズ・問題。良い問題が見つかったときに随時更新する。
四つの点を全て通る3本の線

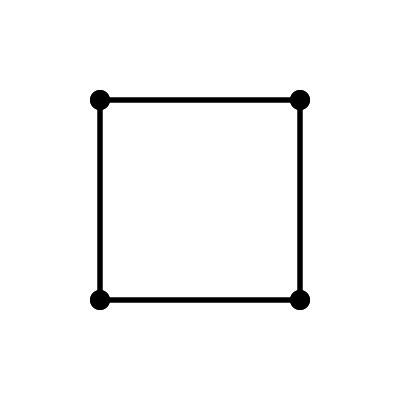
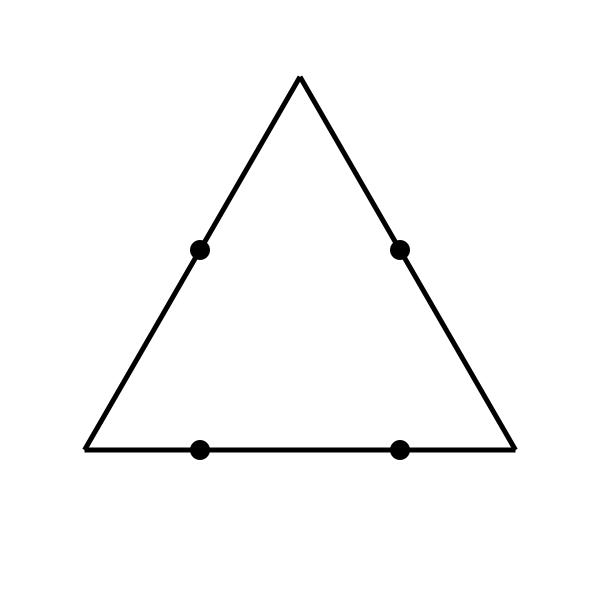
1回の見直しは意味がない
試験では時間が余れば見直しをする。実は1回見直しをして修正するのは意味がない。2回見直しをして、最初に解いた時と合わせて2回異なる回答になったら訂正するのが良い。
1回見直しをして訂正する場合
最初に問題を解くときも見直しをするときも間違える確率をpとする。
見直しをしない場合、正しい回答を書ける確率は 1-p。
1回見直しを行なって、見直しをしたときに正しいと思った方に訂正する場合、正しい回答を書ける確率は 1-p。
2回見直しをして、2回とも最初の回答と異なるものが正解だと思ったときに訂正する場合
最初と合わせて全部で3回同じ問題を解くことになる。間違える確率をpとする。
回答が間違えてしまう確率は、
$$3p^2-2p^3$$
になる。以下の表のように間違える確率が0.5より小さければ、最終的な回答が間違える可能性もより小さくなる。
| 間違える確率(p) | 最終的な回答を間違える確率(3p^2-2p^3) |
| 0 | 0 |
| 0.1 | 0.028 |
| 0.2 | 0.104 |
| 0.3 | 0.216 |
| 0.4 | 0.352 |
| 0.5 | 0.5 |
| 0.6 | 0.648 |
| 0.7 | 0.784 |
| 0.8 | 0.896 |
| 0.9 | 0.972 |
| 1 | 1 |



Comments